本文共 1790 字,大约阅读时间需要 5 分钟。
一.论文解读
论文链接:
1. P、R、O网络结构图解

2. 流程图解
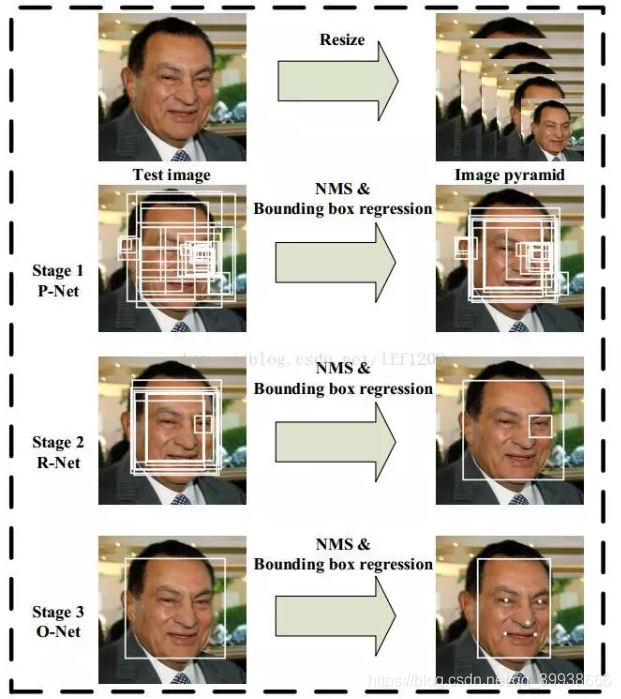
3. 代码实现步骤:
样本预处理(数据集用celeba,拿来先生成3种尺寸12*12/24*24/48*48,每种尺寸含正、负、部分3类) ——> 写P、R、O网络——> 训练网络,得到pkl权重文件 ——> 测试。
其中,测试流程详述:
①先是P网络:
输入任意大小的图(min(w,h) >= 12),img转data并升到4维——>经 _cls, _offest = self.pnet(img_data)得置信度与偏移量,取置信度大于阈值0.6的,得到经边框回归(平移、缩放的逆操作)操作后,即原图的人脸附近可能的预测框坐标集合p_boxes.append
(self.box_reg(idx.cpu().data.numpy(), offset, cls[idx[0],idx[1],idx[2],idx[3]].cpu().data.numpy(),scale))。继续金字塔操作,补充boxes——>NMS。
②传入R网络:
把P得到的这些boxes先补成正方形_pnet_boxes = utils.convert_to_square(pnet_boxes),之后按坐标在原图上把可能是人脸的区域剪下来,再resize到24*24 ——> 经cls, offset = self.rnet(imgdataset)得置信度与偏移量,取置信度大于阈值0.6的。由偏移量求得原建议框坐标集合r_boxes
③传入O网络:
同R流程一样,不同的是阈值由之前的0.5提高到了0.7,结尾的NMS取了isMin=True。
4. 难点
我觉得代码的难点在对于几个方法的理解,如:图像金字塔、交叠度iou、非极大值抑制nms、convert_to_square、边框回归,其中以P网络用到的边框回归方法最难以理解。
那么我就以图像金字塔的理解举个栗子:
图像金字塔并不是训练与测试时都需要的。
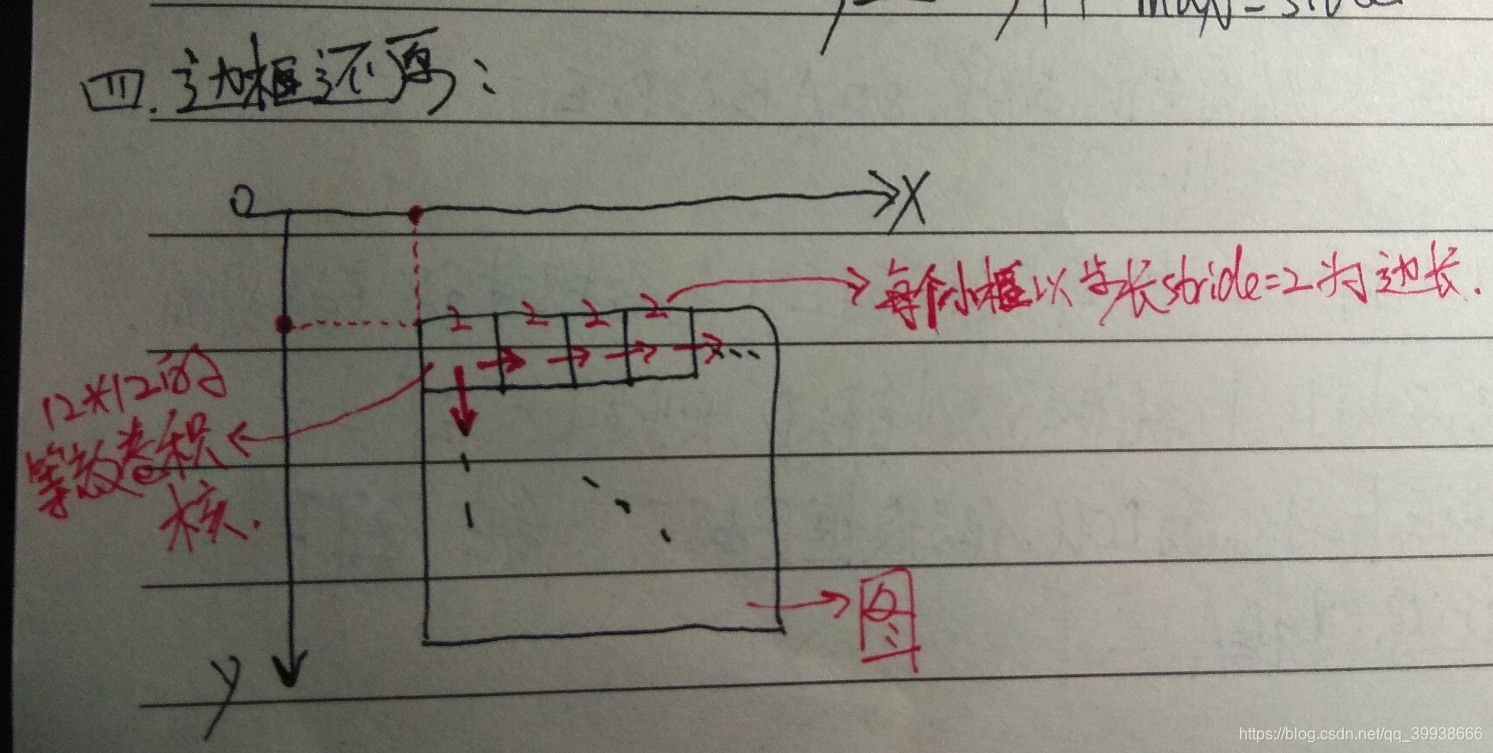
训练阶段不需要,推理阶段需要。训练的时候,需要对训练集中的每个样本缩放到12×12,而对多个尺度的输入图像做训练是非常耗时的,所以为了省时间就没用(没必要用多尺度样本浪费时间)。在推理的时候,测试图像中人脸区域的尺度未知,没有办法,因为P网结构是固定的,当输入图为12*12时,输出的恰好是1*1的5通道特征图,所以可以把p网整体看做一个12*12的卷积核在图片上从左上方开始,取步长stride=2,依次做滑窗操作。——>所以,当刚开始图很大的时候,12*12的框可能只是框住了一张大脸上的某个局部如眼睛、耳朵、鼻子。当该图不断缩至很小的时候,12*12的框能对其框住的也越来越全,直至完全框住了整张脸。
比如一张70*70的图,经过P网全卷积后,输出为(70-2)/2 -2 -2 =30,即一个5通道的30*30的特征图。这就意味着该图经过p的一次滑窗操作,得到了30*30=900个建议框,而每个建议框对应1个置信度cond与4个偏移量offset。再经nms(非极大值抑制:通过iou,把不是极大值的值全都杀掉)把cond大于设定的阈值0.6对应的建议框保留下来,将其对应的offset经边框回归操作,得到在原图中的坐标信息,即得到符合p网的这些建议框了。之后再传给R网。
其他的就先不一 一解释了,给大家推荐几个我认为有助细节理解的博客:
测试流程
细节探讨
图像金字塔
边框回归方法
IOU方法
NMS方法
二. 难点图解
1. iou

2. nms

3. convert_to_square

4. 边框回归box_reg
关键是要理解P网络本身可以看做是一个12*12的大卷积核,以步长stride=2在全图做滑窗。

三.效果图展示
1.原图

2.经过P网络,得到的建议框p_boxes如图

3.然后经过R网络筛选,余下的建议框r_boxes如图

4.最后经过O网络筛选,留下的最终建议框o_boxes如图

后续进度展望:深度学习领域的目标检测主要经历了R-CNN, Fast R-CNN, Faster R-CNN ——> Yolo v1 ,接着一方面走向了SSD、Yolo v2、Yolo v3,另一方面走向了MTCNN等。接下来,博主准备依次研究Yolo系列的3个版本,敬请期待后续更新吧~
转载地址:http://trpi.baihongyu.com/